Compound Interest Formula
Compound interest (or
compounding interest) is interest calculated on the initial principal and also on the accumulated interest of previous
periods of a deposit or loan. Thought to have originated in 17th-century Italy, compound interest can be thought of as “interest on
interest,” and will make a sum grow at a faster rate than simple interest, which is calculated only on the principal
amount. The rate at which compound interest accrues depends on the frequency of compounding; the
higher the number of compounding periods, the greater the compound interest.
Thus, the amount of compound interest accrued on $100 compounded at 10%
annually will be lower than that on $100 compounded at 5% semi-annually over
the same time period.
Compound Interest Formula
P = principal amount (the initial amount you borrow or deposit)
r = annual rate of interest (as a decimal)
t = number of years the amount is deposited or borrowed for.
A = amount of money accumulated after n years, including interest.
n = number of times the interest is compounded per year
Example:
An amount of $1,500.00 is deposited in a bank paying an annual interest rate of 4.3%, compounded quarterly. What is the balance after 6 years?
Solution:
Using the compound interest formula, we have that
P = 1500, r = 4.3/100 = 0.043, n = 4, t = 6. Therefore,
So, the balance after 6 years is approximately $1,938.84.
P = principal amount (the initial amount you borrow or deposit)
r = annual rate of interest (as a decimal)
t = number of years the amount is deposited or borrowed for.
A = amount of money accumulated after n years, including interest.
n = number of times the interest is compounded per year
|
An amount of $1,500.00 is deposited in a bank paying an annual interest rate of 4.3%, compounded quarterly. What is the balance after 6 years?
|
| Using the compound interest formula, we have that P = 1500, r = 4.3/100 = 0.043, n = 4, t = 6. Therefore,
So, the balance after 6 years is approximately $1,938.84.
|
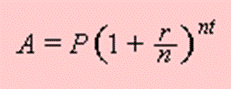
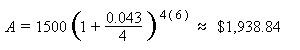
No comments:
Post a Comment