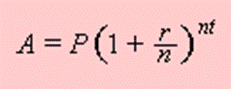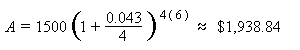Compound Interest Formula

Compound interest (or compounding interest) is interest calculated on the initial principal and also on the accumulated interest of previous periods of a deposit or loan. Thought to have originated in 17th-century Italy, compound interest can be thought of as “interest on interest,” and will make a sum grow at a faster rate than simple interest, which is calculated only on the principal amount. The rate at which compound interest accrues depends on the frequency of compounding; the higher the number of compounding periods, the greater the compound interest. Thus, the amount of compound interest accrued on $100 compounded at 10% annually will be lower than that on $100 compounded at 5% semi-annually over the same time period.

Compound Interest Formula

P = principal amount (the initial amount you borrow or deposit) r  = annual rate of interest (as a decimal) t  = number of years the amount is deposited or borrowed for. A = amount of money accumulated after n years, including interest. n  =  number of times the interest is compounded per year

Example:

An amount of $1,500.00 is deposited in a bank paying an annual interest rate of 4.3%, compounded quarterly. What is the balance after 6 years?

Solution:

Using the compound interest formula, we have that P = 1500, r = 4.3/100 = 0.043, n = 4, t = 6. Therefore, So, the balance after 6 years is approximately $1,938.84.